9504.美好的梦境(二)
Time Limit: 3s Memory Limit: 256MB又是空虚的一天,老师已经不知道这是第几次了。看着眼前作为值日生的 Serika,他始终无法忘记她上一次的遭遇。千千万万不要重蹈上一位的覆辙,老师自思道。Serika 注意到了老师的心思,她决定通过美好的梦境来帮助他重整旗鼓。
老师有 $n$ 个关于学生的梦境,编号为 $1,2,3,\cdots,n$。它们作为节点构成了一棵有根树。编号为 $i$($1\le i\le n$)的梦境拥有 $k_i$ 个儿子梦境,编号分别为 $p_{i,1},p_{i,2},p_{i,3},\cdots,p_{i,k_i}$。
【现在,对于每个编号为 $i$($1\le i\le n$)的梦境以及整数 $j$($1\le j\le k_i$),记 $a_{i,j}=j$。】
老师认为:
- 编号为 $p_{i,a_{i,j}}$($1\le i\le n$,$1\le j\le k_i$)的非根梦境的 左梦境 为编号为 $p_{i,a_{i,\max(j-1,1)}}$ 的梦境,右梦境 为编号为 $p_{i,a_{i,\min(j+1,k_i)}}$ 的梦境。(根据定义,一个非根梦境的左梦境或右梦境均可以是它本身)
- 编号为 $i$($1\le i\le n$)的非叶子梦境的 真儿子梦境 为编号为 $p_{i,a_{i,1}}$ 的梦境。
为了帮助老师重新品味这些梦境,Serika 从 Koyuki 手里购买了三种 Millennium Science School 监制的梦境转移器,分别记作 ←、→ 和 ↓。通过阅读说明书,老师得知了执行这三种梦境转移器所产生的效果:
- 转移器 ← 的效果是:若当前所处梦境是根梦境,不移动,否则移动至它的左梦境。【老师有 $l$ 个这样的转移器。】
- 转移器 → 的效果是:若当前所处梦境是根梦境,不移动,否则移动至它的右梦境。【老师有 $r$ 个这样的转移器。】
- 转移器 ↓ 的效果是:若当前所处梦境是叶子梦境,不移动,否则移动至它的真儿子梦境。【老师有 $d$ 个这样的转移器。】
【老师现在处于梦境 $s$,他想要依照某种顺序执行这些转移器,使得最终移动到的梦境编号最大。老师不喜欢浪费,故 所有转移器都需要被执行,不能有剩余。老师会进行 $q$ 次模拟,其中每次他会钦定 $l,r,d$ 的值,并找来了你帮忙计算对于每一次模拟,通过他的要求最终可以移动到的梦境编号的最大值。出于一些考虑,他只需要你提供与模拟的答案有关的两个值 $xor,sum$。】
Input Format(From the terminal/stdin)
本题包含多组测试数据。
提示:本题输入输出量较大,对于使用 C++ 语言参加竞赛的选手,强烈建议使用关闭同步流的 cin 和 cout 完成输入输出。
首先在第一行输入一个整数 $T$($1\le T\le12$)表示测试数据组数。
对于每一组测试数据,输入包含 $n+q+1$ 行。
第一行包含三个整数 $n,q,s$($1\le n,q\le 4\times10^4$,$1\le s\le n$),分别表示梦境的数量,模拟的次数和梦境的起点。
接下来 $n$ 行,第 $i+1$($1\le i\le n$)行首先包含一个整数 $k_i$($0\le k_i\lt n$)表示梦境 $i$ 的儿子梦境个数。接下来包含 $k_i$ 个整数 $p_{i,1},p_{i,2},p_{i,3},\cdots,p_{i,k_i}$($1\le p_{i,1},p_{i,2},p_{i,3},\cdots,p_{i,k_i}\le n$),表示梦境 $i$ 的儿子梦境。
接下来 $q$ 行,每行包含三个整数 $l,r,d$($0\le l,r,d\le l+r+d\le4.5\times10^4$),分别表示三种转移器的数量。
保证输入的梦境构成一棵有根树。
Output Format(To the terminal/stdout)
对于每一组测试数据,输出包含一行两个整数 $xor,sum$,表示特殊的输出方式所需要的两个值。
具体地,$xor,sum$ 满足以下条件:
$$xor=\oplus_{i=1}^{q}ans_i\times i$$
$$sum=\sum_{i=1}^{q}ans_i\times i$$
其中 $ans_i$ 是第 $i$ 次模拟的答案,$\oplus$ 表示二进制按位异或。
Sample Input
2 3 3 2 2 3 2 0 0 0 1 0 1 0 1 1 1 1 11 4 4 0 0 0 4 6 5 10 7 1 11 1 1 2 9 8 0 0 2 3 2 0 0 0 2 0 721 3 0 1 1 0 721 1\n · · \n · · \n \n \n · · \n · · \n · · \n · · \n \n \n \n · · · · \n · \n · \n · · \n \n \n · · \n \n · · \n · · \n · · \n · · \n
Sample Output
13 17 45 81· \n · \n
Hints
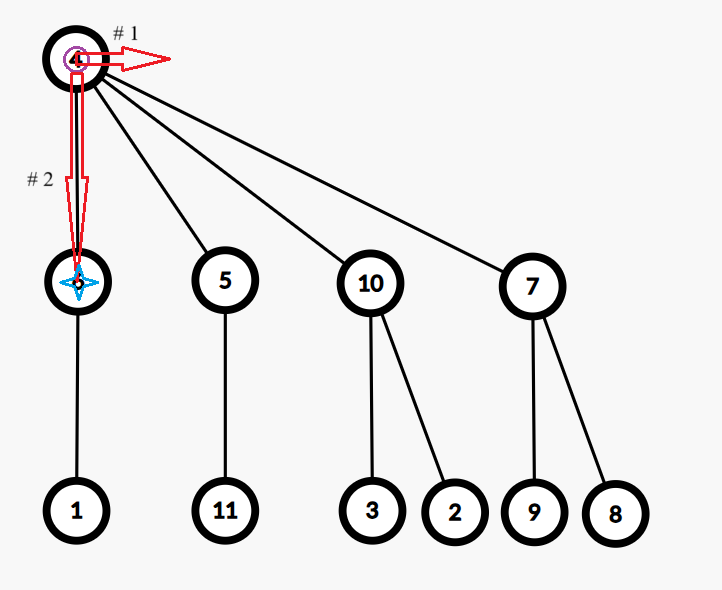
以下参考图中,紫色圆圈标记的梦境表示起点梦境,红色箭头表示每次移动(箭头旁的标号表示这次移动对应着第几个被执行的转移器),蓝色四角星标记的梦境表示最终到达的梦境。
这个样例共有两组测试数据。
在第一组测试数据中,梦境共有 $3$ 个,共有 $3$ 次模拟。起点梦境的编号为 $2$。
-
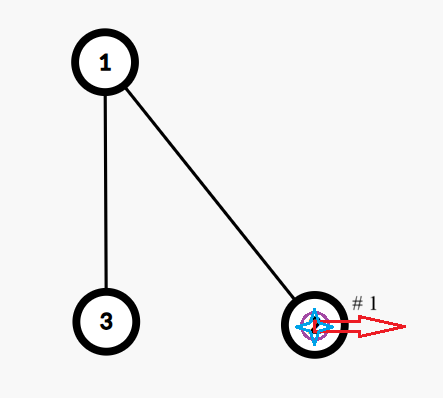
第 $1$ 次模拟钦定 $l=0,r=1,d=0$。执行 →。答案为 $2$。
-
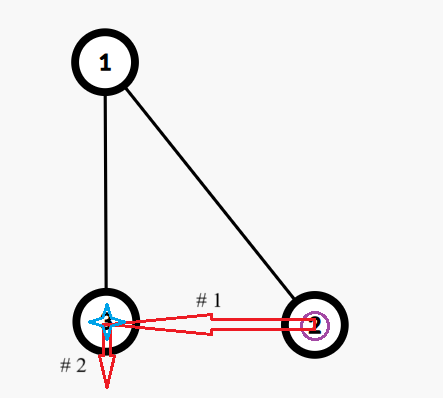
第 $2$ 次模拟钦定 $l=1,r=0,d=1$。执行 ←↓。答案为 $3$。(只列出一种达到最大值的方案)
-
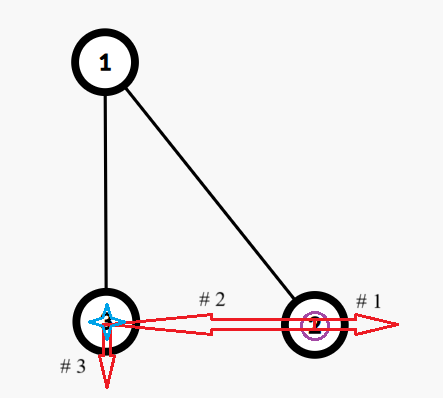
第 $3$ 次模拟钦定 $l=1,r=1,d=1$。执行 →←↓。答案为 $3$。(只列出一种达到最大值的方案)
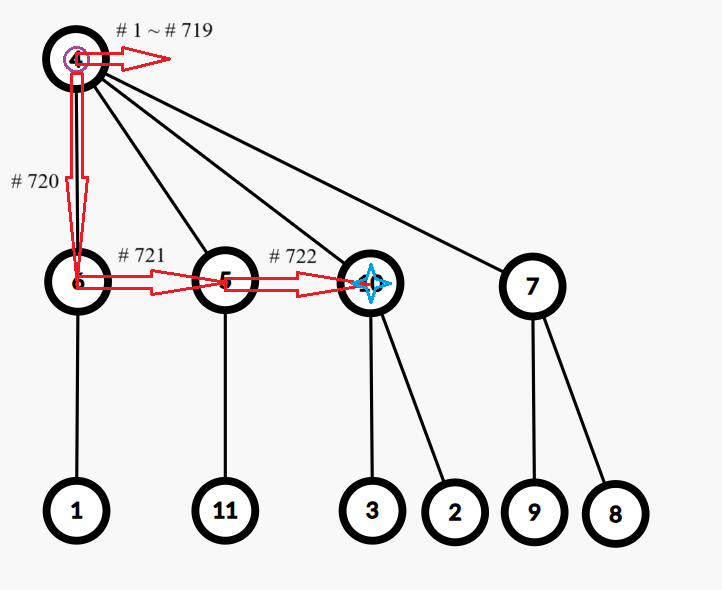
在第二组测试数据中,梦境共有 $11$ 个,共有 $4$ 次模拟。起点梦境的编号为 $4$。
- 第 $1$ 次模拟钦定 $l=0,r=0,d=2$。执行 ↓↓。答案为 $1$。
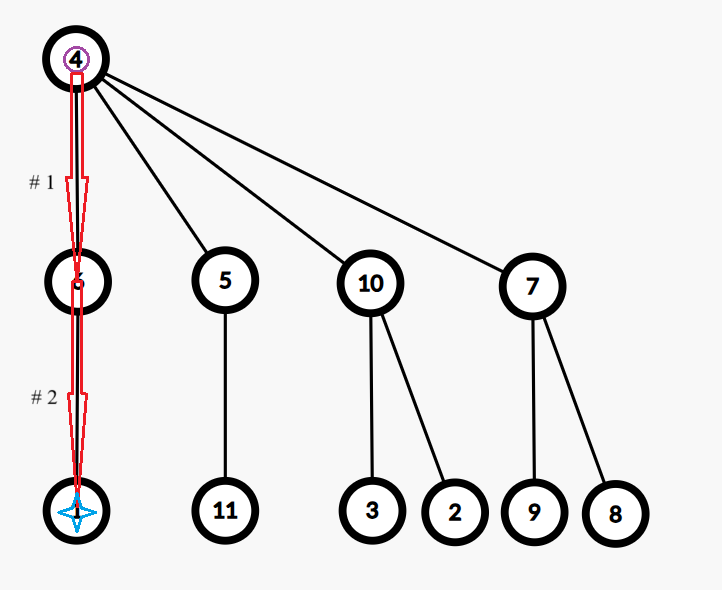
- 第 $2$ 次模拟钦定 $l=0,r=721,d=3$。执行 ↓→↓↓,再执行 $720$ 个 →。答案为 $11$。(只列出一种达到最大值的方案)
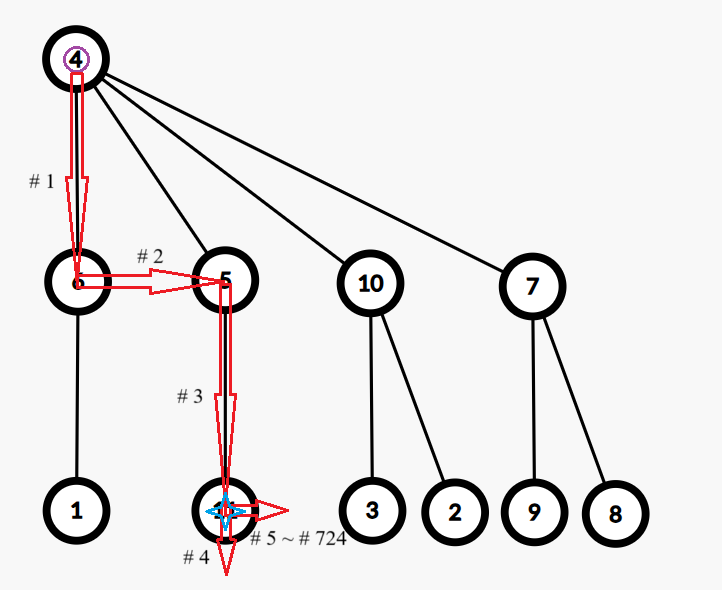
- 第 $3$ 次模拟钦定 $l=0,r=1,d=1$。执行 →↓。答案为 $6$。
- 第 $4$ 次模拟钦定 $l=0,r=721,d=1$。执行 $719$ 个 →,再执行 ↓→→。答案为 $10$。