给定一张 简单有向图 $G$ 包含编号为 $1,2,3,\cdots,n$ 的点。此图包含 $m$ 条边，编号为 $1,2,3,\cdots,m$，其中第 $i$（$1\le i\le m$）条边为 $u_i\to v_i$。

定义有向图 $G^0$ 是一张包含两个编号分别为 $1,2$ 的点与一条边 $1\to2$ 的图。对于整数 $k$（$k\ge 1$），定义有向图 $G^k$ 是将 $G^{k-1}$ 中的每一条边使用 $G$ 同时替换所得到的图（可见 样例解释 中的参考图）。替换时将 $G^{k-1}$ 中的每一条边的起点视为 $G$ 中编号为 $1$ 的点，终点视为 $G$ 中编号为 $2$ 的点。

具体地，对于正整数 $k$，按下面的方式构造有向图 $G^k$：

1. 首先使 $G^k$ 中包含与 $G^{k-1}$ 相同数目的点，并给它们分配与 $G^{k-1}$ 相同的编号。此时 $G^k$ 中不包含任何边。
2. 对于 $G^{k-1}$ 中的每条有向边，轮流执行一次添加操作。
3. 给 $G^k$ 中的点重新分配连续正整数编号。

一次对 $G^{k-1}$ 中的有向边 $u\to v$ 的添加操作如下：

1. 在 $G^k$ 中加入 $n$ 个新点，并按照图 $G$ 的方式在这 $n$ 个新点之间连接 $m$ 条有向边。设这 $n$ 个新点中，与图 $G$ 中编号为 $1,2$ 的点对应的点的编号分别是 $x,y$。
2. 在 $G^k$ 中找到编号为 $u,v$ 的点。合并编号为 $u,x$ 的点、编号为 $v,y$ 的点。合并编号为 $a,b$ 的点时，把所有形如 $b\to\gamma$ 的边修改为 $a\to\gamma$，把所有形如 $\gamma\to b$ 的边修改为 $\gamma\to a$。由于不可能出现 $a\to b$ 与 $b\to a$，所以不需要考虑。允许出现重边。

如果你还是不理解这个过程，可以参考 样例解释 的伪代码。

给定图 $G$ 和非负整数 $k'$，计算 $G^{k'}$ 中的强连通分量的个数。对 $1000000007$ 取模。

本题包含多组测试数据。

首先在第一行输入一个整数 $T$（$1\le T\le100$）表示测试数据组数。

对于每一组测试数据，输入包含 $m+1$ 行。

第一行包含三个整数 $n,m,k'$（$2\le n\le 10^5$，$2\le\sum n\le 3\times 10^5$，$0\le m\le\sum m\le10^6$，$0\le k'\le 10^{18}$），分别表示 $G$ 中点与边的数量，以及与计算答案有关的参数。

接下来 $m$ 行，第 $i+1$（$1\le i\le m$）行包含两个整数 $u_i,v_i$（$1\le u_i,v_i\le n$）表示一条 $G$ 中的边 $u_i\to v_i$。

保证输入的点与边构成一张简单有向图。（即无重边与自环）

对于每一组测试数据，输出包含一行一个整数表示 $G^{k'}$ 中强连通分量个数对 $1000000007$ 取模后的值。

在样例的第二组测试数据中，将 $G^1$ 中的每一条边使用 $G$ 同时替换的过程如下图所示（其中黑色虚线边表示 $G^1$ 中的边 $u'\to v'$，这条边仅作指示作用，在 $G^2$ 中不存在，仅一部分图中绘制了黑色虚线边）：

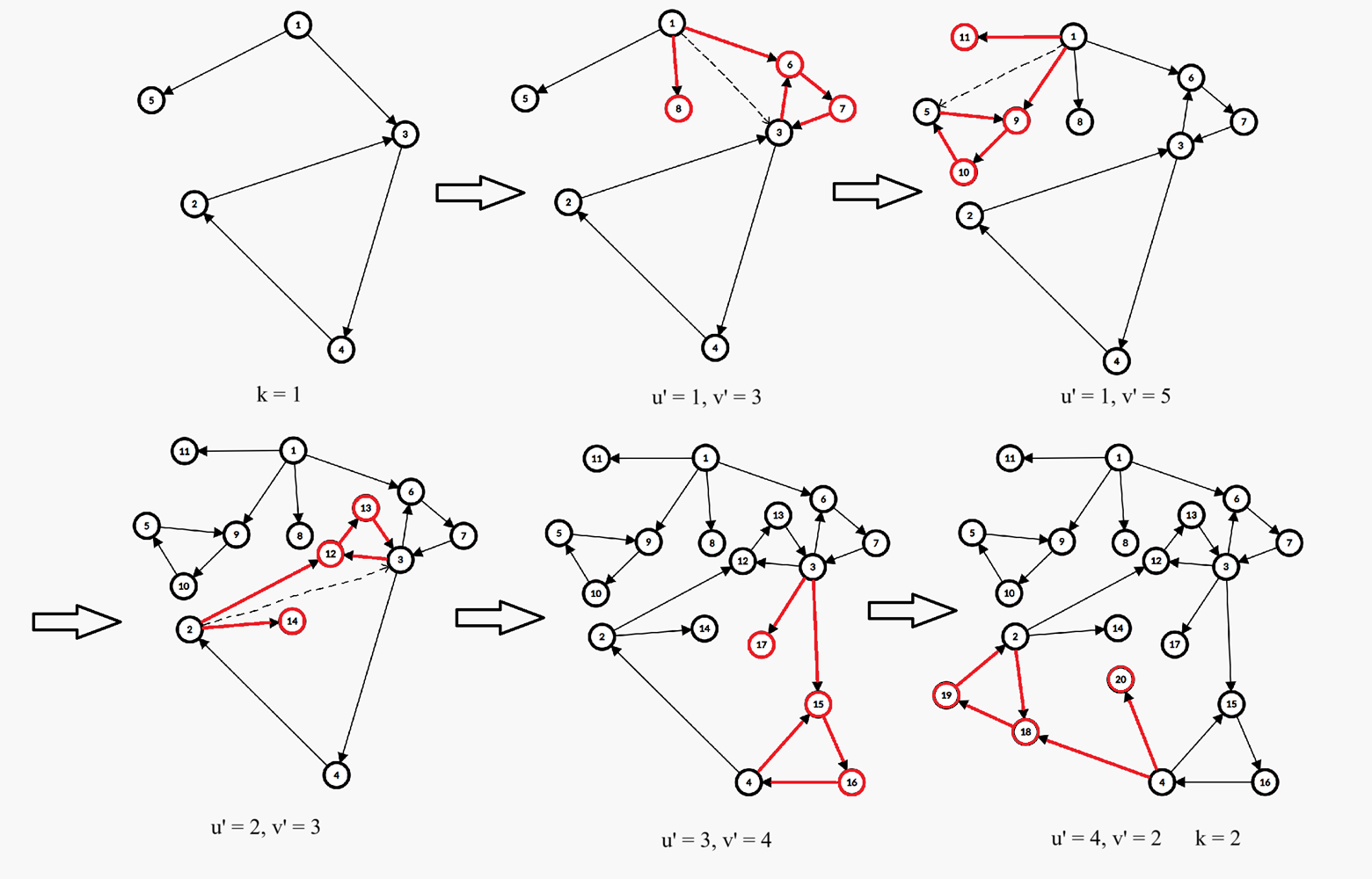
答案为 $8$。

在这里给出伪代码，伪代码以图 $G$ 和整数 $k$ 作为输入，返回图 $G^k$：