龙穴是龙族的栖息地，它由无限多个正六边形房间铺成。如下图所示，任何一个房间都可以用三维坐标（$q,r,s$）（$q,r,s\in\mathbb{Z}$, $q+r+s=0$）表示；黄色房间的坐标为（$0,0,0$）；房间（$q,r,s$）周围一圈 6 个房间顺时针依次为：（$q,r-1,s+1$）、（$q+1,r-1,s$）、（$q+1,r,s-1$）、（$q,r+1,s-1$）、（$q-1,r+1,s$）、（$q-1,r,s+1$）。

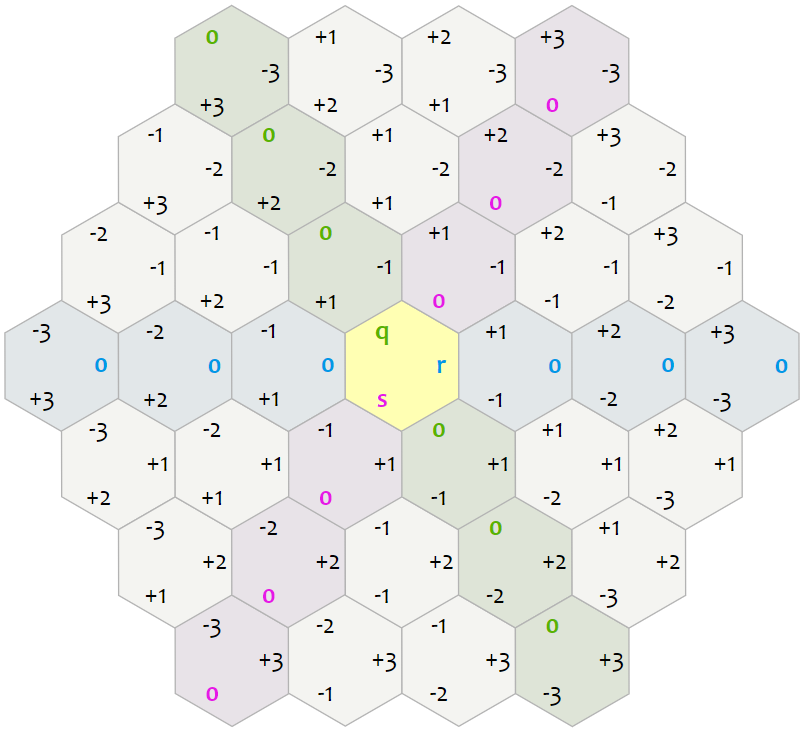
龙穴中一共栖息着 $n$ 条龙，第 $i$ 条龙位于（$q_i,r_i,s_i$），一个房间可以有多条龙。一条龙一步只能从当前房间移动到相邻房间。龙族准备选择一个房间（该房间可以没有龙）作为龙穴的核心，使得所有 $n$ 条龙移动到该房间所需的最少步数之和尽可能小，请写一个程序帮助龙族确定龙穴核心房间的位置。

第一行包含一个正整数 $T$（$1\leq T\leq 300$），表示测试数据的组数。

每组数据第一行包含一个正整数 $n$（$2\leq n\leq 100\,000$），表示栖息在龙穴中的龙的数量。

接下来 $n$ 行，每行三个整数 $q_i,r_i,s_i$（$|q_i|,|r_i|,|s_i|\leq 10^9$, $q_i+r_i+s_i=0$），分别表示每条龙所在的房间。

输入数据保证 $\sum n\leq 1\,000\,000$。

对于每组数据输出一行一个整数，即所有 $n$ 条龙移动到核心房间所需的最少步数之和。