Kou 今天要准备一张图招待 Hikari 和 Tairitsu 这对好朋友，然而三个人对图的结构不同的要求，更具体地，对于一张简单无向正权图而言：

• Kou 要保证 Hikari 和 Tairitsu 保持平衡不打架，所以保证图上任意两个简单环的边权和相等。
• Hikari 喜欢 $3$，因此她要求每个点度数不超过 $3$。
• Tairitsu 不喜欢 $3$，因此她要求任意两点间简单路径数不是 $3$ 的倍数。

于是 Kou 画了一张符合三个人要求的简单无向正权图。后来 Kou 想要隐藏图里美好的性质，她将其中一部分边的权值改成了新的权值（新权值可能为 $0$）。因此，修改之后原本美好的性质可能就不存在了。

现在她们给出Kou 修改完后的图，同时给出多组询问，每次询问 $S,T$ 间所有简单路径中，边权异或和最大的那条。

第一行读入三个整数 $ n,m,q $（$2\le n\le 10^6$，$1\le m \le 1.5\times 10^6$，$1\le q\le 5\times 10^4$），表示图的点数、边数和询问组数。

接下来 $m$ 行，每行三个整数 $u,v,w$ 表示一条 $u,v$ 之间边权为 $w$（$ 0\le w < 2^{16} $）的边。

再接下来 $q$ 行，每行两个整数 $S,T$ 表示一组询问。保证 $S\ne T$。

输出 $q$ 行，对于每组询问，输出边权异或和的最大值。

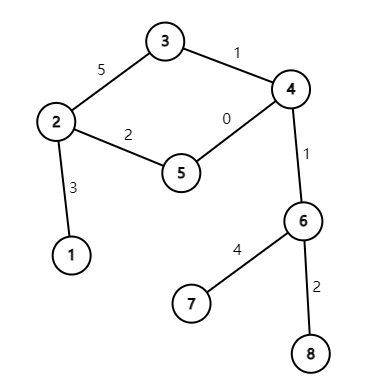
如果我们用 $\oplus$ 表示异或，那么：

• 第一次询问 $7,8$ 间边权异或和最大值，这两点间只有一条简单路径 $7-6-8$，异或和为 $4\oplus 2=6$。
• 第二次询问 $1,7$ 间边权异或和最大值，这两点间有两条简单路径 $1-2-3-4-6-7$ 和 $1-2-5-4-6-7$，边权异或和分别是 $2$ 和 $4$，其中较大值为 $4$。
• 第三次询问 $3,5$ 间边权异或和最大值，这两点间有两条简单路径 $3-2-5$ 和 $3-4-5$，边权异或和分别是 $7$ 和 $1$，其中较大值为 $7$。