9563.计算几何
Time Limit: 5s Memory Limit: 512MB给定一个网格图和一个闭合不自交的折线,问应该如何使用尽可能少的钉子和一条弹性圈来模拟出这条折线。钉子的半径忽略不计。
Input Format(From the terminal/stdin)
第一行包含一个正整数 $T$($1\le T\le 100$),表示数据组数。
对于每一组数据,第一行包含一个正整数 $n$($3\le n\le 5\times 10^5$,$\sum n\le 5\times 10^5$),表示折线中折点的数目。
接下来 $n$ 行,每行包含两个整数 $ x_i, y_i $($-2\times 10^9 \le x_i, y_i \le 2\times 10^9$),表示第 $i$ 个点的坐标(点的编号从 $1$ 到 $n$)。
这边的折线指的就是 $ (x_1,y_1) - (x_2,y_2) - \ldots - (x_n,y_n) - (x_1,y_1)$。注意:不保证任意三个相邻的点不共线。
Output Format(To the terminal/stdout)
对于每一组数据,输出正整数 $k$ 表示至少使用 $k$ 个钉子,然后按照 $x$ 从小到大,$x$ 相同的时候按照 $y$ 从小到大的顺序输出这 $k$ 个钉子的位置,同时输出这个钉子是否被折线“包裹”住。(如果是输出 YES 反之输出 NO)
> 我们定义一个点被折线“包裹”住为:这个点在这个折线形成的多边形内。
Sample Input
Copy
2 6 0 1 1 4 2 2 3 3 4 0 1 2 7 0 2 1 2 2 2 1 0 2 0 3 1 2 3\n \n · \n · \n · \n · \n · \n · \n \n · \n · \n · \n · \n · \n · \n · \n
Sample Output
Copy
6 0 1 YES 1 2 NO 1 4 YES 2 2 NO 3 3 YES 4 0 YES 6 0 2 YES 1 0 YES 2 0 YES 2 2 NO 2 3 YES 3 1 YES\n · · \n · · \n · · \n · · \n · · \n · · \n \n · · \n · · \n · · \n · · \n · · \n · · \n
Hints
使用尽可能少的钉子和一条弹性绳来模拟出样例中的折线的方案分别为:
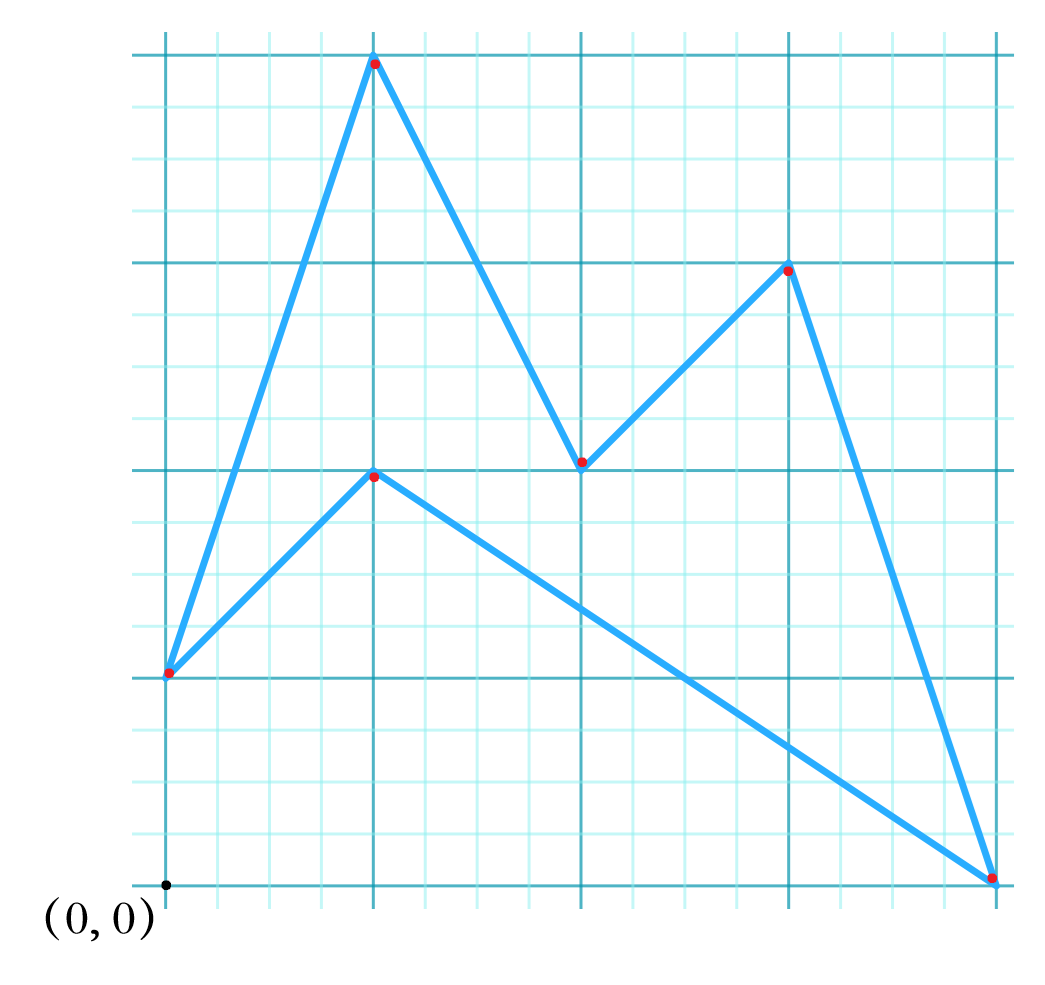
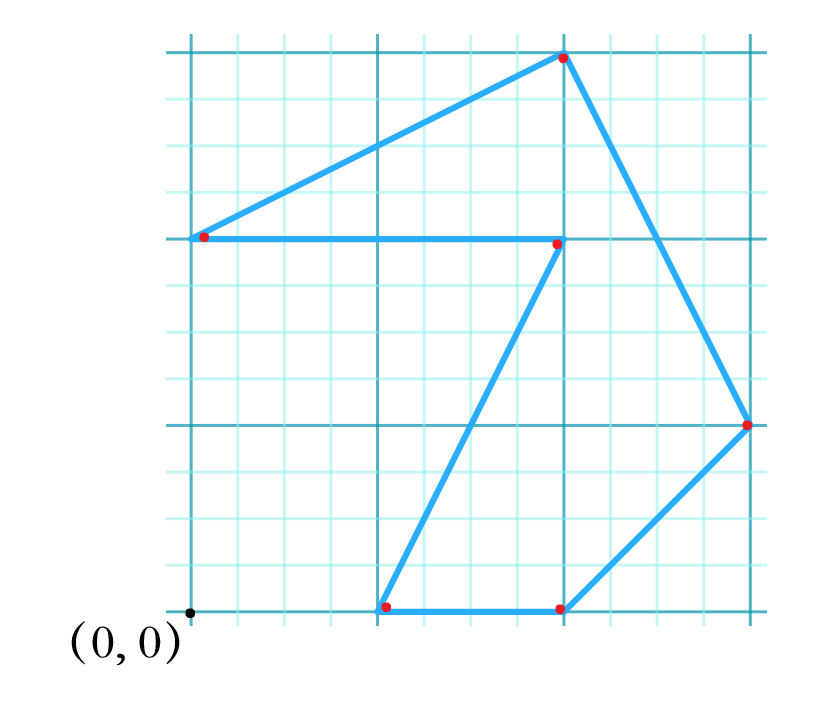
Source: 2025“钉耙编程”中国大学生算法设计暑期联赛(9), HDU, 8079
Submit
请先 登录