一战期间，战争被和平打破。

那是在 1914 年「西方战线」的圣诞节， 尽管有着严格的军令不准他们与敌方士兵谈笑风生， 英国和德国的军人们却都离开了他们的战壕，穿过了无人地带， 聚集在了一起，来埋葬他们的战友、交换礼物、有的还玩起了游戏。

相比之下，现在已经是 2025 年，西方世界已经保持了好几十年的和平，我们，诶？我们信任彼此的能力简直太差了。有调查表明，在过去的四十年当中，越来越少的人说他们「信任彼此」。所以，我们难免会有这样的疑问：

为什么朋友会变成敌人，即使在和平年代也不例外呢？

为什么敌人也会变成朋友，而且这种事居然在战争年代也会发生？

你正在进行一个信任游戏：

你面前有一台机器。两个人都可以选择「合作」，放一枚硬币；或者「欺骗」，不放硬币。不妨假设玩家初始都有足够数量的硬币，具体得到硬币如下表：（注意表中的收益是包括你可能放进去的硬币的）

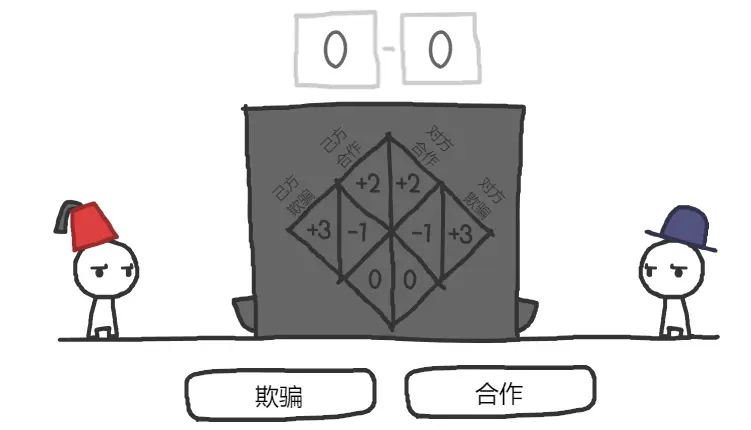
两位玩家每一步操作都是同时进行的。因此，每个人的选择不会因为对方本轮的选择而改变，而是取决于对方之前轮的选择。

一局游戏会进行 $m$ 轮。现在有 $n$ 个玩家，他们各自都有固定的游戏策略。每个玩家的游戏策略可以用一个长度为 $m$ 的字符串序列 $a$ 表示，其中 $a_1\in \begin{Bmatrix}\verb!T,C!\end{Bmatrix}$，对于 $2\le i\le m$，满足 $a_i\in \begin{Bmatrix}\verb!T,C,R!\end{Bmatrix}$。在第 $i$ 轮时，策略与 $a_i$ 关系如下：

• 若 $a_i=\verb!T!$，则第 $i$ 轮该玩家选择「合作」；
• 若 $a_i=\verb!C!$，则第 $i$ 轮该玩家选择「欺骗」；
• 若 $a_i=\verb!R!$，则第 $i$ 轮该玩家会与对方的上一轮选择相同。

现在任意两位不同玩家之间会进行恰好一局游戏。你想知道，所有游戏结束后，每个玩家得到（或失去）了多少硬币。

本题有多组数据。第一行一个正整数 $T$（$1\le T\le 5$），表示测试数据组数。

接下来 $T$ 组数据。对于每组数据，第一行两个正整数 $n,m$（$1\le n,m\le 10^5$，$1\le n\cdot m\le 10^7$）。

接下来 $n$ 行，每行为一个长度为 $m$ 的字符串，表示第 $i$ 个玩家的策略。

保证 $\sum n\cdot m\le 4\cdot 10^7$。

输出一行 $n$ 个整数，第 $i$ 个表示第 $i$ 个玩家得到了多少硬币。

若第 $i$ 个玩家失去了 $x$（$x>0$）个硬币，那么你应当输出 $-x$。

...你可能有点怀疑我开头讲的那个一战战壕里圣诞节休战的故事。那真的只是一个小概率事件吗？

没错，休战看起来还是挺戏剧化的，但是既不能说是独一无二的，也不能说是不寻常。

并不是每一个战壕都会达成和平，然而这种现象还是挺普遍的。尽管，我再次强调，有着明确和严格的军令禁止，但是许多前线部队都会不约而同地达成和平。

而且事实上，即使在圣诞节之前，有一些前线部队就已经悄悄地达成了非官方的和平。

他们把这个叫做：「互惠宽容（live and let live）」系统。本质上来讲，就是你不打我，我也就不打你。而且这种情况在很多地方都适用。

你可能还会有疑惑。一般士兵并不会自发地与敌人达成和平，为什么这种情况在当谈到战壕里作战的阵地战时就格外不同了呢？

那是因为，阵地战这样一个特点：它跟其他形式的战役不同，在阵地战中，你每天都会面对的是同一批军人。

这是一个重复游戏。这一点使得阵地战与其他的战争完全不同。

在样例第二组数据中的硬币最多的玩家，策略是第一局「合作」，之后一直按照对手上一局的动作。

我们把这样的玩家称为复读机。复读机也有很多别名。像什么黄金准则啦，互惠利他主义啦，以牙还牙啦，或者说互惠宽容。这就是为什么「和平」会如雨后笋子一般在一战的战壕中蔓延开来：当你被迫每天与同一批人——不是仅仅是普遍意义上的「敌人」而是同样的一批人——进行同样的游戏（例如战争）时，复读机这样的人不单单会赢得一场战役——

他们会赢得整场战争。

文案来源：信任的进化